Как построить дерево в виде графа

Древовидный граф - распространенная структура данных в программировании и часто применяемая в алгоритмах. Содержимое этой структуры тяжело поддается исследованию во время отладки, в силу того, что практически всегда описывается одним узлом ссылающимся на своих потомков. Т.е. чтобы получить значение некоторого узла, приходится выполнять нетривиальный обход дерева. И тут на помощь может придти визуальное представление такого графа. Построение графа в виде компактного и легко воспринимаемого дерева, задача нетривиальная и имеет безусловно множество решений. В статье хотелось бы поделиться собственным "колесом" для решения этой задачи.

В статье подразумевается, что в любой момент времени можно получить информацию о потомках конкретного узла дерева. Ссылки на узел-предок не обязательны, т.к. присутствуют не во всех представлениях деревьев.

Код в статье представлен на языке Java. Чтобы код был понятен читателю, не знакомому с java, вкратце опишу используемые классы, специфичные для языка:

• Point - описывает точку с координатами x и y;
• Dimension - описывает размер. Содержит поля hight и width;
• Rectangle - описывает прямоугольник его размерами и координатами верхнего левого угла;
• TreeModel - описывает дерево. Позволяет получать потомков и их количество для конкретного узла.

Главным требованием к алгоритму, было минимальное количество обходов дерева для вычисления координат каждого узла.

Идея предлагаемого решения заключается в том, чтобы рассматривать в качестве потомка не узел в отдельности, а все порождаемое им дерево целиком:

Введем понятие "грозди". Гроздь - это некоторая структура данных, ссылающаяся на узел дерева и имеющая ссылки на такие же "грозди", соответствующие потомкам этого узла.

В задачи грозди входит вычисление параметров области расположения узла, на который она ссылается и вычисление собственных габаритов.

По сути, гроздь - это карта размещения узла и его потомков.

Создание гроздей и вычисление координат верхнего левого их угла выполняется при рекурсивном обходе дерева в глубину:

    
        ...
Object rootNode = getRootNode();
createBunch(rootNode, new Point(0, 0));
        ...
/**
  * Рекурентно создает грозди для узла и его потомков.
  * 
  * @param userNode
  *            узел дерева.
  * @param p
  *            координата верхнего левого узла грозди.
  * @param horizontalMargin
  *            горизонтальное расстояние между узлами дерева. 
  * @param verticalMargin
  *            вертикальное расстояние между узлами дерева.
  * @return гроздь созданную для переданного узла.
  */        
Bunch createBunch(Object userNode, Point p, int horizontalMargin, int verticalMargin) {
    Bunch bunch = new Bunch(p, userNode, nodeDimention, horizontalMargin, verticalMargin);
    if (!isLeaf(userNode)) {
        p.y += nodeDimention.height + verticalMargin;
        for (int i = 0; i < getChildCount(userNode); i++) {
            Object child = getChild(userNode, i);
            Bunch m = createBunch(child, new Point(p), horizontalMargin, verticalMargin);
            bunch.addChild(m);
            p.x += m.getExternalBoundary().width + horizontalMargin;
        }
    }
    return bunch;
}
   

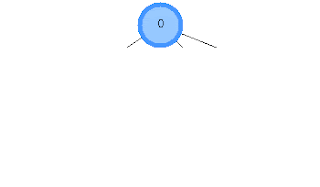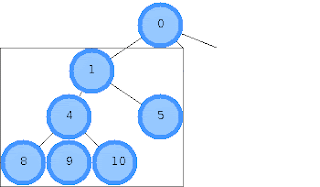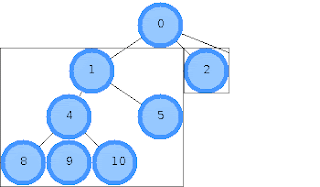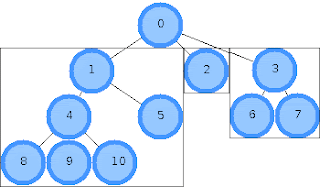
Для наглядного изображения идеи, рассмотрим пример вычисления координат потомков корневого узла 0. Алгоритм подразумевает, что к этому моменту координаты узлов 4-10 уже вычислены, и габариты деревьев, порождаемых узлами 1, 2 и 3 известны(горизонтальное расстояние между ячейками в примере равно 0):

+

+

=

Координаты областей для отрисовки узлов дерева вычисляются при добавлении потомков к грозди:

   /**
 * Добавляет гроздь в список потомков.
 * @param child 
 *            гроздь ссылающаяся на потомка узла текущей грозди.
 */
public void addChild(Bunch child) {
    // Первый потомок определяет ширину грози
    if (children.size() == 0) {
        externalBoundary.width = child.getExternalBoundary().width;
    // Каждый последующий увеличивает ширину грози на ширину добавляемой грозди + 
    // горизонтальное расстояние между узлами
    } else {
        externalBoundary.width += child.getExternalBoundary().width + margin.width;
    }
    // Область размещения узла, соответствующего грозди, размещается посередине грозди
    nodeBoundary.x = externalBoundary.x + externalBoundary.width / 2
            - nodeBoundary.width / 2;

    // Высота грозди вычисляется как сумма самой высокой грозди среди потомков,
    // высоты ячейки и вертикального расстояния между ячейками
    if (child.getExternalBoundary().height > maxChildHeight) {
        maxChildHeight = child.getExternalBoundary().height;
    }
    externalBoundary.height = nodeBoundary.height + margin.height + maxChildHeight;

    children.add(child);
}
   

Предлагаемое решение позволяет достаточно быстро проверить попадание точки в один из узлов дерева(при первом вызове метода getTreeNode, в качестве аргумента b указывается гроздь, соответствующая корневому узлу дерева):

/**
 * @param p
 *            точка на дереве.
 * @param b
 *            гроздь, в которой выполняется поиск.
 * @return узел, в который попадает точка или null, если точка не попадает ни в какой
 *         из узлов.
 */
Object getTreeNode(Point p, Bunch b) {
    if (!b.getExternalBoundary().contains(p)) {
        return null;
    }
    if (b.getNodeBoundary().contains(p)) {
        return b.getUserNode();
    }
    Iterator<Bunch> itr = b.children();
    while (itr.hasNext()) {
        Bunch child = itr.next();
        Object node = getTreeNode(p, child);
        if (node != null) {
            return node;
        }
    }
    return null;
}

Исходный код класса Bunch

       /**
 * Гроздь (карта узла). Содержит область для отображения самого узла, а также список карт
 * его потомков. Выполняет важную функцию вычисления размеров грозди (узел и его потомки).
 * 
 * @author dok
 * @see http://www.dokwork.ru/2012/10/treemap.html
 */
class Bunch {

    /**
     * Возвращает ссылку на узел дерева.
     */
    public Object getUserNode() {
        return userNode;
    }

    /**
     * Возвращает границу узла дерева. Узел должен отрисовываться в рамках этой границы.
     */
    public Rectangle getNodeBoundary() {
        return nodeBoundary;
    }

    /**
     * Возвращает границу грозди.
     */
    public Rectangle getExternalBoundary() {
        return externalBoundary;
    }

    /**
     * Возвращает итератор по списку потомков узла, представленных гроздями.
     */
    public Iterator<Bunch> children() {
        return children.iterator();
    }

    /**
     * Добавляет гроздь в список потомков.
     * 
     * @param child
     */
    public void addChild(Bunch child) {
        /* Recalculate width */
        if (children.size() == 0) {
            externalBoundary.width = child.getExternalBoundary().width;
        } else {
            externalBoundary.width += child.getExternalBoundary().width + margin.width;
        }
        nodeBoundary.x = externalBoundary.x + externalBoundary.width / 2
                - nodeBoundary.width / 2;

        /* Recalculate height */
        if (child.getExternalBoundary().height > maxChildHeight) {
            maxChildHeight = child.getExternalBoundary().height;
        }
        externalBoundary.height = nodeBoundary.height + margin.height + maxChildHeight;

        children.add(child);
    }

    /**
     * Создает гроздь.
     * 
     * @param p
     *            верхний левый угол грозди.
     * @param dim
     *            размер области для изображения узла.
     * @param margin
     *            отступы между узлами.
     */
    public Bunch(Point p, Object userNode, Dimension dim, Dimension margin) {
        this.userNode = userNode;
        this.margin = margin;
        externalBoundary = new Rectangle(p, dim);
        nodeBoundary = new Rectangle(p, dim);
        children = new ArrayList<Bunch>();
    }

    private Object userNode;

    private Rectangle nodeBoundary;

    private Rectangle externalBoundary;

    private Dimension margin;

    private List<Bunch> children;

    private int maxChildHeight = 0;
}
       
       

Исходный код класса TreeMap

/**
 * Описывает расположение узлов дерева.
 * 
 * @author dok
 * @see http://www.dokwork.ru/2012/10/treemap.html
 */
public class TreeMap {

    /**
     * Возвращает область отображения узла.
     * 
     * @param userNode
     *            узел дерева.
     * @return область отображения узла.
     */
    public Rectangle getNodeBoundary(Object userNode) {
        return map.get(userNode).getNodeBoundary();
    }

    /**
     * Возвращает размер области для отображения дерева.
     * 
     * @return размер области для отображения дерева.
     */
    public Dimension getSize() {
        return map.get(treeModel.getRoot()).getExternalBoundary().getSize();
    }

    /**
     * Возвращает узел дерева в который попадает указанная точка или null, если точка не
     * попадает ни в один из узлов.
     * 
     * @param p
     *            точка.
     * @return узел дерева или null.
     */
    public Object getNode(Point p) {
        Object rootNode = treeModel.getRoot();
        Bunch m = map.get(rootNode);
        return getTreeNode(p, m);
    }

    /**
     * Возвращает описание дерева.
     * 
     * @return модель дерева.
     */
    public TreeModel getTreeModel() {
        return treeModel;
    }

    /**
     * Устанавливает модель дерева.
     * 
     * @param treeModel
     *            модель дерева.
     */
    public void setTreeModel(TreeModel treeModel) {
        if (treeModel == null) {
            throw new IllegalArgumentException("TreeModel can't be null.");
        }
        this.treeModel = treeModel;
        map = new HashMap<Object, Bunch>();
        Object rootNode = treeModel.getRoot();
        addNodeToMap(rootNode, new Point(0, 0));
    }

    /**
     * Возвращает размер ячеек.
     */
    public Dimension getNodeSize() {
        return nodeSize;
    }

    /**
     * Устанавливает размер узлов дерева. Приводит к перерасчету всей карты.
     * 
     * @param nodeSize
     *            размер узла.
     */
    public void setNodeSize(Dimension nodeSize) {
        this.nodeSize = nodeSize;
        setTreeModel(treeModel);
    }

    /**
     * Возвращает вертикальное расстояние между узлами дерева.
     */
    public int getVerticalMargin() {
        return verticalMargin;
    }

    /**
     * Устанавливает вертикальное расстояние между узлами дерева. Приводит к перерасчету
     * всей карты.
     * 
     * @param verticalMargin
     *            вертикальное расстояние между узлами дерева.
     */
    public void setVerticalMargin(int verticalMargin) {
        this.verticalMargin = verticalMargin;
        setTreeModel(treeModel);
    }

    public int getHorizontalMargin() {
        return horizontalMargin;
    }

    /**
     * Устанавливает горизонтальное расстояние между узлами дерева. Приводит к перерасчету
     * всей карты.
     * 
     * @param horizontalMargin
     *            горизонтальное расстояние между узлами дерева.
     */
    public void setHorizontalMargin(int horizontalMargin) {
        this.horizontalMargin = horizontalMargin;
        setTreeModel(treeModel);
    }

    /**
     * Создает описание расположения узлов дерева.
     */
    public TreeMap() {
        this.map = new HashMap<Object, Bunch>();
        /* Устанавливаются значения поумолчанию */
        this.nodeSize = new Dimension(30, 30);
        this.horizontalMargin = 5;
        this.verticalMargin = 20;
    }

    /**
     * Создает описание расположения узлов дерева.
     * 
     * @param model
     *            описываемая модель дерева.
     */
    public TreeMap(TreeModel model) {
        this();
        setTreeModel(model);
    }

    /**
     * Рекурентно создает грозди для узла и его потомков, добавляя грозди в карту.
     * 
     * @param userNode
     *            узел дерева.
     * @param p
     *            координата верхнего левого узла грозди.
     * @return гроздь созданную для переданного узла.
     */
    private Bunch addNodeToMap(Object userNode, Point p) {
        Bunch bunch = new Bunch(p, userNode, nodeSize, new Dimension(horizontalMargin,
                verticalMargin));
        map.put(userNode, bunch);
        if (!treeModel.isLeaf(userNode)) {
            p.y += nodeSize.height + verticalMargin;
            for (int i = 0; i < treeModel.getChildCount(userNode); i++) {
                Object child = treeModel.getChild(userNode, i);
                Bunch m = addNodeToMap(child, new Point(p));
                bunch.addChild(m);
                p.x += m.getExternalBoundary().width + horizontalMargin;
            }
        }
        return bunch;
    }

    /**
     * Выполняет рекурсивный поиск узла, содержащего указанную точку.
     * 
     * @param p
     *            точка на дереве.
     * @param b
     *            гроздь, в которой выполняется поиск.
     * @return узел, в который попадает точка или null, если точка не попадает ни в какой
     *         из узлов.
     */
    private Object getTreeNode(Point p, Bunch b) {
        if (!b.getExternalBoundary().contains(p)) {
            return null;
        }
        if (b.getNodeBoundary().contains(p)) {
            return b.getUserNode();
        }
        Iterator<Bunch> itr = b.children();
        while (itr.hasNext()) {
            Bunch child = itr.next();
            Object node = getTreeNode(p, child);
            if (node != null) {
                return node;
            }
        }
        return null;
    }

    private TreeModel treeModel;

    private Map<Object, Bunch> map;

    private Dimension nodeSize;

    private int verticalMargin;

    private int horizontalMargin;
}

UPD: изложенные в статье идеи были воплощены в компоненте JGraphTree о котором можно почитать в соседней статье: Компонент JGraphTree.